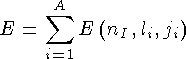
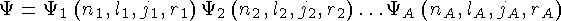
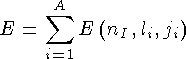
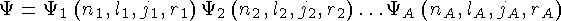
 - заполненная оболочка
- заполненная оболочка
 - одна частица на оболочке
- одна частица на оболочке
2 частицы на оболочке 
|
|
-3/2 |
-1/2 |
1/2 |
3/2 |
|||||
|
-3/2 |
-3 |
-2 |
-1 |
0 |
|||||
|
-1/2 |
-2 |
-1 |
0 |
1 |
|||||
|
1/2 |
-1 |
0 |
1 |
2 |
|||||
|
3/2 |
0 |
1 |
2 |
3 |
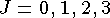
Изотопы
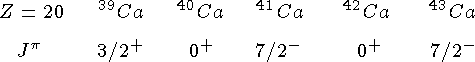
Изотопы
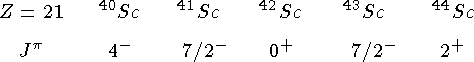
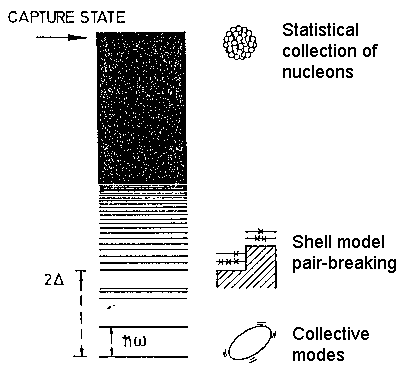
В случае ядра 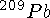 спектр воздужденных
состояний с энергиями до 2 МеВ хорошо интерпретируется
как одночастичный переход нейтрона в оболочке
спектр воздужденных
состояний с энергиями до 2 МеВ хорошо интерпретируется
как одночастичный переход нейтрона в оболочке 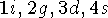 сверх заполненного дважды магического остова
сверх заполненного дважды магического остова 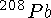 .
.
В модели оболочек нуклоны рассматриваются как независимые частицы
в самосогласованном потенциале, создаваемом всей совокупностью
нуклонов в ядре. Уровни энергии 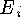 нуклонов определяются собственными
значениями решений уравнения Шредингера
нуклонов определяются собственными
значениями решений уравнения Шредингера
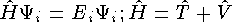
где 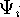 - волновая функция нуклона с энергией
- волновая функция нуклона с энергией 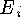 ,
, 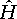 - оператор гамильтона,
- оператор гамильтона,
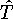 и
и 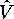 - операторы кинетической и потенциальной энергии.
- операторы кинетической и потенциальной энергии.
Форма потенциала самосогласованного поля зависит от выбора модельного приближения. В одночастичной модели оболочек потенциал сферически симметричного самосогласованного поля имеет вид
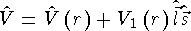
Здесь 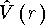 - центральный потенциал, а второе слагаемое описывает спин-орбитальное
взаимодействие. В простейших моделях сферических ядер V(r) имеет вид потенциала
трехмерного гармонического осциллятора
- центральный потенциал, а второе слагаемое описывает спин-орбитальное
взаимодействие. В простейших моделях сферических ядер V(r) имеет вид потенциала
трехмерного гармонического осциллятора
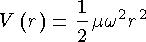
где 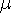 - приведенная масса нуклона, либо прямоугольной потенциальной ямы
- приведенная масса нуклона, либо прямоугольной потенциальной ямы
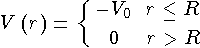
где R - радиус ядра. Более точные решения получены с потенциалом Вудса-Саксона
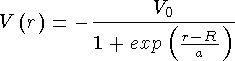
близким по радиальной зависимости к распределению плотности ядра.
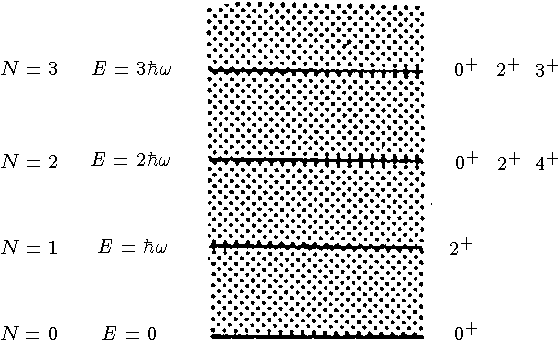
Для потенциала гармонического осциллятора спектр энергетических уровней, приведенных на рисунке, имеет следующий вид:
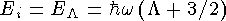
где 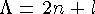 , n - главное квантовое число (число узлов функции, кроме нуля), l -
орбитальное квантовое число. Стационарные состояния трехмерного осциллятора
обозначают символом (n+1)l;
, n - главное квантовое число (число узлов функции, кроме нуля), l -
орбитальное квантовое число. Стационарные состояния трехмерного осциллятора
обозначают символом (n+1)l; 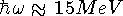 .
.
Волновая функция бесспиновой частицы в поле, обладающем сферической симметрией, имеет вид
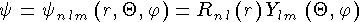
где 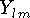 - сферические функции. Вид радиальной функции R зависит от
конкретного вида потенциала V(r)
- сферические функции. Вид радиальной функции R зависит от
конкретного вида потенциала V(r)
Волновая функция нуклона в сферически симметричном поле может быть представлена в виде
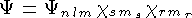
где 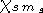 - спиновая функция, причем
- спиновая функция, причем 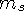 = +1/2 либо -1/2;
= +1/2 либо -1/2; 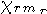 - изоспиновая функция,
- изоспиновая функция,
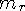 = +1/2 либо -1/2 (протон либо нейтрон).
= +1/2 либо -1/2 (протон либо нейтрон).
Заполнение уровней наклонами в потенциальной яме происходит последовательно, начиная с нижнего уровня в соответствии с принципом Паули.
Учет спин-орбитального взаимодействия, то есть члена 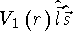 в потенциале
взаимодействия, приводит к расщеплению уровней системы. Стационарное состояние
нуклона кроме квантовых чисел n и l хаарактеризуются также полным моментом
j, то есть
в потенциале
взаимодействия, приводит к расщеплению уровней системы. Стационарное состояние
нуклона кроме квантовых чисел n и l хаарактеризуются также полным моментом
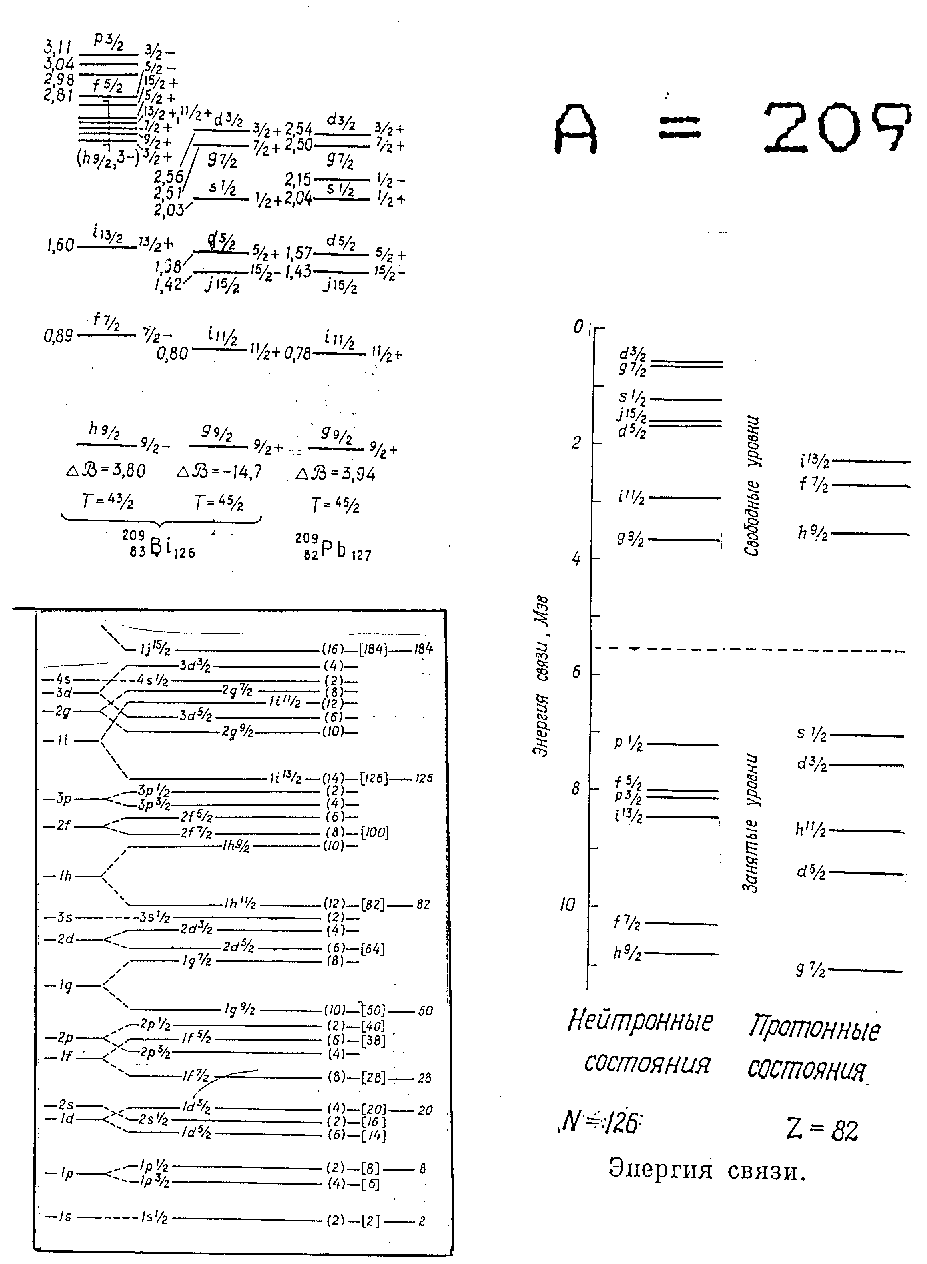
j, то есть 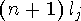 . Приведена схема ядерных уровней прямоугольной потенциальной
ямы (слева - без спин-орбитальной связи, справа - при наличии спин-орбитальной
связи). Для протонов в самосогласованый потенциал должен быть включен также
кулоновский потенциал.
. Приведена схема ядерных уровней прямоугольной потенциальной
ямы (слева - без спин-орбитальной связи, справа - при наличии спин-орбитальной
связи). Для протонов в самосогласованый потенциал должен быть включен также
кулоновский потенциал.
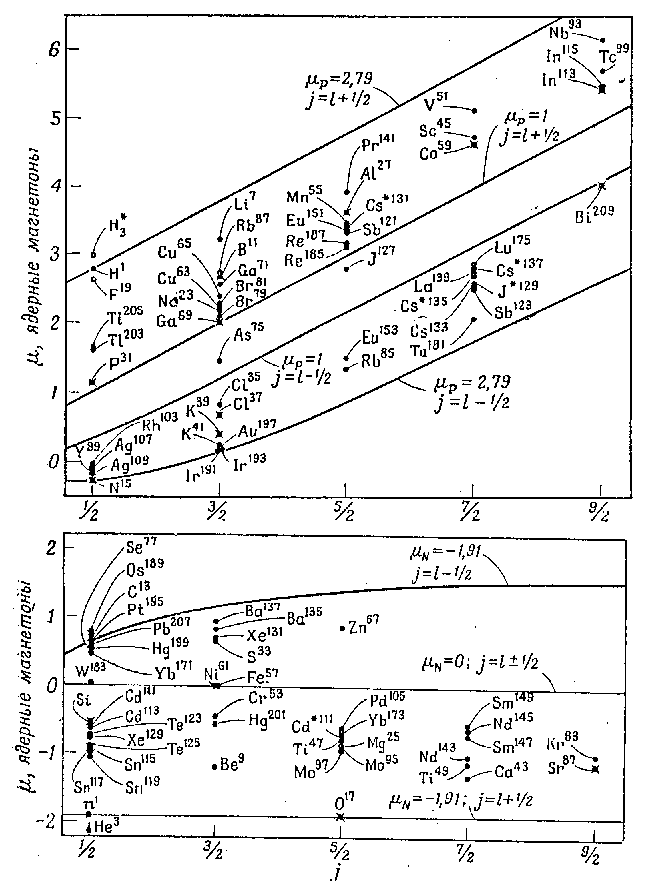
В одночастичной модели оболочек магнитные моменты ядер, близких к сферическим, определяются магнитным моментом неспаренного нуклона.
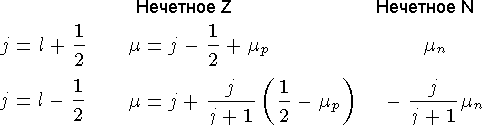
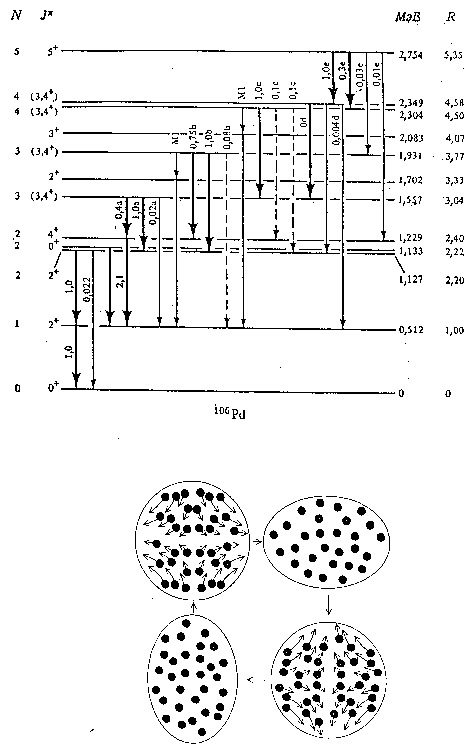
Функцию поверхности геометрической фигуры произвольной формы можно разложить в ряд по
сферическим функциям. Если коэффициенты разложения 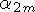 не зависят от времени, то соотношение
описывает постоянную деформацию ядра.
не зависят от времени, то соотношение
описывает постоянную деформацию ядра. 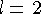 соответствует квадрупольной деформации.
соответствует квадрупольной деформации.
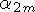 , зависящие от времени, описывают квадрупольные колебания ядра.
, зависящие от времени, описывают квадрупольные колебания ядра.
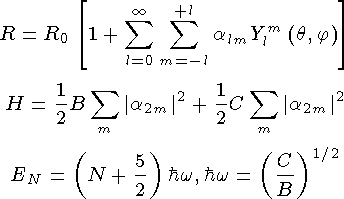
В модели Нильсона деформированное ядро рассматривается как система невзаимодействующих частиц, движущихся в деформированной потенциальной яме.
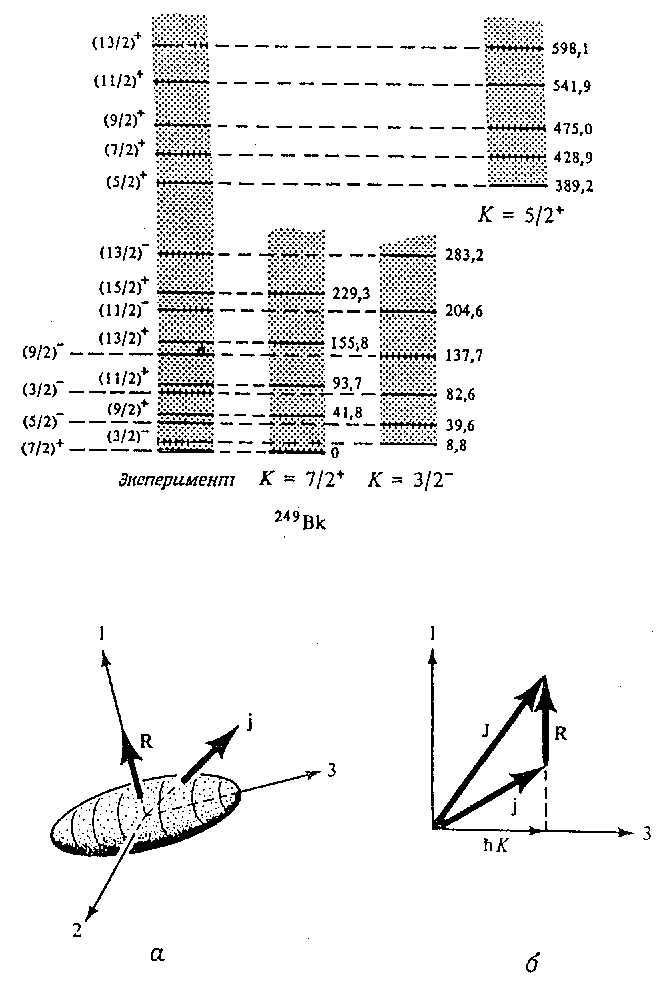
Для деформированных ядер состояние нуклона нельзя характеризовать квантовыми числами l и j. В этом случае момент количества движения, создаваемый нуклоном, следует характеризовать проекцией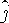 на ось симметрии ядра (рассматриваются
аксиально симметричные ядра). Квантовое число этой проекции k будет принимать
полуцелые значения
на ось симметрии ядра (рассматриваются
аксиально симметричные ядра). Квантовое число этой проекции k будет принимать
полуцелые значения
k = j, j-1, j-2, ..., -j+2, -j+1, -j.
Деформация частично снимает вырождение, присущее одночастичным уровням
сферически симметричного потенциала, расщепляя по энергии состояния с
различными значениями модуля k . В силу аксиальной симметрии состояния с k и
-k остаются вырожденными. Для одночастичных уровней таких ядер используется
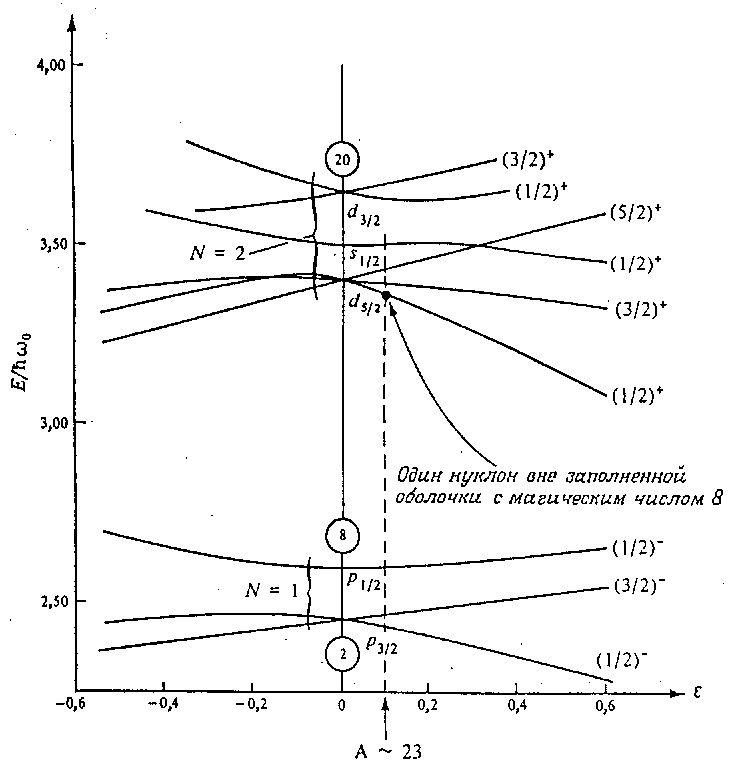
обозначение 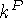 , где P - четность. На схеме показана зависимость энергии
одночастичных уровней для аксиально-симметричного потенциала (потенциала
Нильссона) в зависимости от параметра деформации ядра.
, где P - четность. На схеме показана зависимость энергии
одночастичных уровней для аксиально-симметричного потенциала (потенциала
Нильссона) в зависимости от параметра деформации ядра.
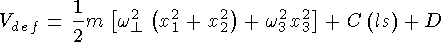
Если состояние валентного нуклона слабо влияет на вращательное состояние остова, то каждое состояние валентного нуклона может стать основным (начальным) для семейства вращательных уровней - вращательной полосы. Все уровни одной вращательной полосы имеют одну и ту же одночастичную структуру и различаются только величиной коллективного вращательного момента.
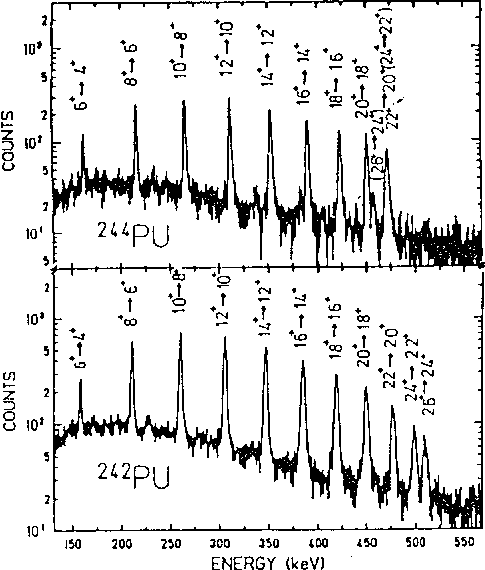
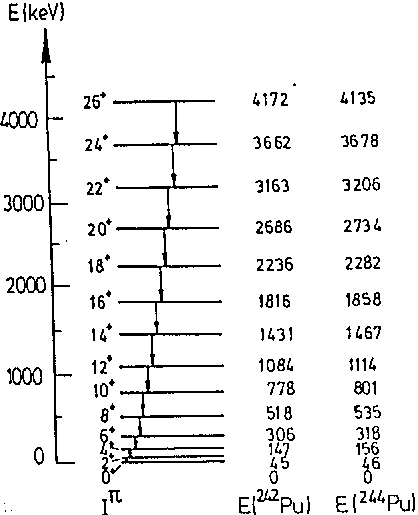
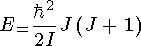
Семейства вращательных уровней
All Your comments, suggestions and bug reports (any kind) are welcome here.
Last updated 13 April 1997 year.